🔺 Area of the Triangle – Explained with Formulas and Easy Examples
Triangles are among the most common shapes in mathematics, engineering, and daily life. Whether you’re a student solving geometry problems, an architect working on designs, or someone needing to measure land or space, understanding how to calculate the area of a triangle is essential.
This guide will explain what a triangle is, the different types, and walk you through three accurate methods to calculate its area — complete with clear examples.
🔺 What is a Triangle?
A triangle is a two-dimensional shape with three sides, three angles, and three vertices. The total of its internal angles is always 180°. It’s a fundamental building block in geometry and forms the basis of many real-world structures and problems.
📚 Types of Triangles
Before jumping into the formulas, let’s understand the types of triangles you might deal with:
- Equilateral Triangle: All sides and angles are equal. Each angle measures 60°.
- Isosceles Triangle: Two sides are equal in length. Two equal angles opposite those sides.
- Scalene Triangle: All three sides and angles are different.
- Right-Angled Triangle: One angle is exactly 90°. Commonly used in trigonometry and physics.
📐 Methods to Calculate Area of a Triangle
There are three widely used methods to calculate the area of a triangle, depending on what information is available:
| Method | What You Need | Formula |
|---|---|---|
| 1. Base & Height | Base and perpendicular height | (1/2) × base × height |
| 2. Heron’s Formula | All three side lengths | √s(s-a)(s-b)(s-c) |
| 3. Trigonometric Method | Two sides and included angle | (1/2) × a × b × sin(C) |
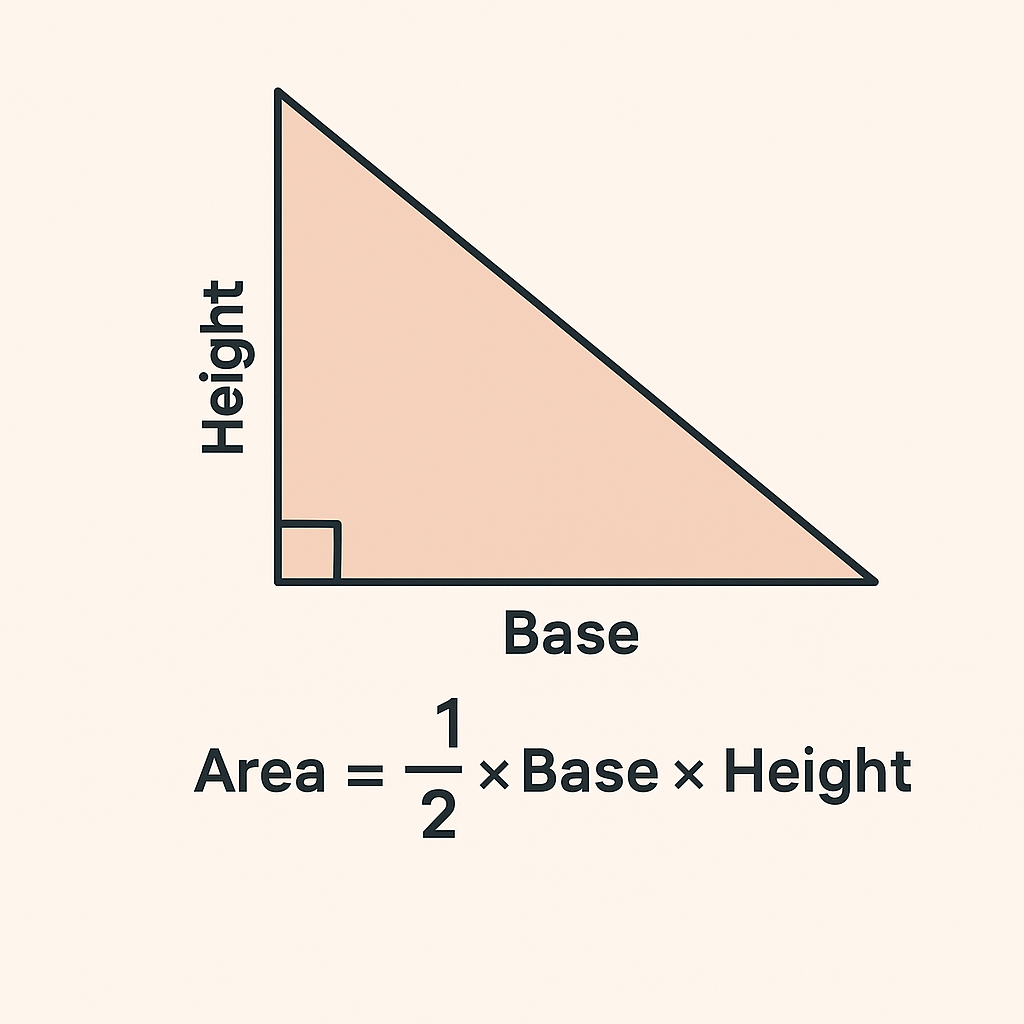
Method 1: Using Base and Height
This is the most straightforward method when the height of the triangle is known.
✅ Formula:
Area = (1/2) × Base × HeightExample:
Let’s say the base of a triangle is 12 cm and the height is 8 cm:
Area = (1/2) × 12 × 8 = 48 cm²🌐 Try Our Free Triangle Area Calculator
Method 2: Heron’s Formula (Using 3 Sides)
If you don’t know the height but have the lengths of all three sides, you can use Heron’s Formula.
✅ Formula:
s = (a + b + c) / 2
Area = √s(s-a)(s-b)(s-c)
Example:
Let’s say a triangle has side lengths of 7 cm, 9 cm, and 10 cm:
s = (7 + 9 + 10) / 2 = 13
Area = √[13(13-7)(13-9)(13-10)]
= √(13 × 6 × 4 × 3)
= √936 ≈ 30.6 cm²
Method 3: Trigonometric Method (2 Sides + Angle)
If you know two sides and the included angle (the angle between the two sides), this method is best.
✅ Formula:
Area = (1/2) × a × b × sin(C)Example:
Let’s say:
- Side a = 10 cm
- Side b = 6 cm
- Angle C = 30°
Area = (1/2) × 10 × 6 × sin(30°)
= 30 × 0.5 = 15 cm²